Here is Chantal's simulation once again. Readers can judge for themselves who is really making "sprinkled noise" here.
Classical Spheres, Division Algebras, and the Illusion of Quantum Non-locality:
Let me point out the dishonesty in some of the assertions behind Mr. Moldoveanu's claims about Chantal's and Michel's simulations. I have done the same for his false claims about my analytical model many times before, so I won't bother with that here (in any case, it has been verified by many competent physicists by now, such as Lucien Hardy).
To begin with, in the real experiments what is observed is what is predicted by quantum mechanics (if anyone claims otherwise, then they have observed actual violations of quantum mechanics and deserve a Nobel Prize). Quantum mechanics does not predict individual outcomes observed at one of the two stations. It predicts *probabilities* of observing *simultaneous* occurrences of measurement events at the two stations. Accordingly, in actual experiments what is observed are *coincidences* of measurement events. For example, coincidences of results A = +1 by Alice and B = -1 by Bob. This means that what is actually observed are simultaneous occurrences like {A = +1, B = -1}. Or, equivalently, AB = -1. The question then is: what are the probabilities of observing AB = +1 and AB = -1?. That is what is predicted by quantum mechanics, and that is what is observed. And---and here is the point---that is what is predicted by my analytical model, and that is what is simulated by Chantal in her simulation. Of course, one can try to observe results only at Alice's station. But then all we find is 50/50 occurrence of A = +1 and A = -1, and that is trivial to simulate. So the dishonest claim made about "experimental outcomes" is just that---dishonest. It smuggles-in something that is not even predicted by quantum mechanics, let alone actually observed.
I have already commented on the dishonest claims made by Mr. Moldoveanu about Michel's simulation. His main dishonesty there is to neglect the actual random variable (or the actual initial state), which is the set {e, t}, and consider only e, so that he can misinterpret the simulation according to his own whim.
I have already commented above on the dishonest claims made by Mr. Moldoveanu about Michel's simulation. His dishonesty is to neglect the actual random variable (or the actual initial state), which is the set {e, t}, and consider only e, so that he can misinterpret the simulation according to his own whim.
Detector efficiency, detection rate, unfair bias, fair or unfair sampling, are all completely irrelevant once the correct initial state {e, t} is correctly taken into account.
" ... by simply using a linear progressive bias the correlation curves can approach the QM curve."
Florin, one can take any of the machine languages separately in which Joy's measurement framework has been simulated, and bias it toward a linear result. This is a limitation of all machine languages (difference vs. differential) to simulate a continuous function.
The truly surprising and meaningful result of transporting the algorithm to four different programming languages is evidence that *the simulation of a continuous function is a continuous function.* That is, every time we use classically random input regardless of the program language, we get a smooth continuum of correlated points. This makes the simulated measurement framework a true nonlinear simulation of continuously random input -- in other words, random input to a 3 dimension simulation generates a 4 dimension reality, which is the one in which we live.
Florin, programming skill -- and even the debatable efficiencies of programming languages -- is entirely irrelevant.
The *science* of the simulation outcome is independent of computer results. Until you (and Vongehr and Gill) understand the meaning of a measurement function continuous from an initial condition, you are getting nowhere toward understanding why quantum correlations are a natural result of continuous classically random nonlinear input to the measurement function.
Hi Jonathan,
"So in a way; the Octonions had to exist, for the Reals to come to be."
This is the kind of thing that makes mathematicians crazy :-) -- we don't tend to think that "pi in the sky" is real, until confronted with the consistency of numerical results that should live in disconnected spaces.
It is one thing to speak of simply-connected spaces in an objective, abstract, mathematical way. To have evidence of that physical reality (Joy's measurement framework), is a wonderful leap in intellectual history.
All best,
Tom
Florin,
Let me try and explain it this way:
Your consistent misspelling of Michel's name ("Michael") illustrates how languages differ in linearly ordered terms without affecting the meaning. The French spelling Michel means the same thing as the English transliteration of the Hebrew name Michael. Same goes for the Spanish Miguel and the Russian Mikhail.
The scientific meaning of a continuous measurement function simulation is indifferent to how the terms are linearly ordered. What we want to find out, is what happens when totally disordered elements of reality are subjected to a classically random function (coin-toss probability) -- is the result more disorder (noise), or newly ordered relations (information, such as names found in a look-up table)?
What we see is that the probability -- given a function continuous from the initial condition -- that the function generates ordered relations, is exactly the same as the probability for quantum correlations under the assumption of linear superposition (with implications for nonlocality and probability theory).
It makes the difference between a probabilistic measure schema on a disconnected space, and a deterministic classically random and continuous measure space. Christian's measure space assumes only initial condition and a measurement function continuous from the initial condition. That assumption cannot be made on the real line of ordered relations -- it requires the nonlinearity that we witness in almost all natural phenomena. The inescapable conclusion is the lack of boundary between quantum and classical domains.
Indeed!
The basic idea that there are persistent structures in Math, invariant regardless of how we approach or approximate them, seems alien to many. However, if one digs into the Math deeply enough; this seems to happen again and again - to a point where it seems undeniable that there is some pre-existing order to Math, that must appear no matter how it is probed.
That is the wonder of things like Frobenius' conjectures and the Hurwitz theorem, or the Poincare conjecture proof. The results definitively show that certain things believed to be separate or separable are intrinsically linked by the very nature of higher-order numbers and geometry.
It is unavoidable! Specific higher-order numbers and spaces MUST exist; and if higher-order spaces exist in any form, they MUST observe some specific geometric properties. This is hard for many people to wrap their heads around, however.
Regards,
Jonathan
Also to mention..
The nature of continuous number fields is different in kind from discrete numbers. If we observe the behavior of squaring over the positive Reals, endlessly iterated, only a value of 1 is stable - and any increment more or less, no matter how small, begins a steady march to either 0 or infinity. Zero, one, and infinity (the point that's typically forgotten), sounds familiar.
This result for multiplication also implies the inverse for division - infinite divisibility - which is part of the significance of the normed division algebras. In my view; their existence is the whole basis for reversibility, and symmetries, and finite groups, and a whole lot of other things considered essential to Physics.
More later,
Jonathan
Jonathan,
"It is unavoidable! Specific higher-order numbers and spaces MUST exist; and if higher-order spaces exist in any form, they MUST observe some specific geometric properties. This is hard for many people to wrap their heads around, however."
This may be mathematician talk, but, just in case: Are you saying that there exists actual physical volumes, your 'spaces', in addition to but external to our observed universe? Is it a higher dimensional reality that: "This is hard for many people to wrap their heads around?
James Putnam
This is amazing to me.
Except for some technical programming questions in sci.physics.foundations (which have been addressed and disposed of) I see only internet silence on this simulation that critics IIRC universally said is a prerequisite to having Joy's measurement framework taken seriously.
As they say in American baseball -- what are you waiting for, egg in your beer?
Tom
Tom,
As you may recall, many completely bogus claims were made about my local-realistic framework by those committed to Bell's theorem. This wrongfully undermined my perfectly sound work, misled the physics community, and damaged my scientific reputation. Do you see anyone coming out now and saying that they were wrong? What does that tell you about the true intentions of those who made the wrongful claims? What does that tell you about their scientific and moral integrity? What does that tell you about their ability to judge a perfectly sound work that goes against their cherished beliefs?
Best,
Joy
Joy, I agree. One has to have a personal agenda aside from the good of science to behave this way. Some made their agenda obvious from the beginning. I can't find any excuse for the others.
Leon Lederman and Dick Teresi asked, "If the universe is the answer, what is the question?"*
Non-Realists such as Anton Zeilinger imply that there are no questions at a foundational level. "Zeilinger says that some of the alternative non realist possibilities are truly weird. For example, it may make no sense to imagine what would happen if we had made a different measurement from the one we chose to make. 'We do this all the time in daily life,' says Zeilinger -- for example, imagining what would have happened if you had tried to cross the road when a truck was coming. If the world around us behaved in the same way as a quantum system, then it would be meaningless even to imagine that alternative situation, because there would be no way of defining what you mean by the road, the truck, or even you."
Zeilinger assumes -- as do all Bell's theorem adherents -- that the definition of objects precedes the measurement of correlations between objects. It should be no surprise, therefore, that the assumption of quantum entanglement generates a measurement result based merely on the definition of itself. The proof of the theorem is a nonconstructive tautology.
What Bell loyalists neglect is that there *is* no way of objectively " ... defining what you mean by the road, the truck, or even you." And there doesn't need to be. The realism of continuous functions does not depend on discrete definitions -- in every experiment purporting to show quantum entanglement and violation of Bell/CHSH inequalities, the experimenter and the apparatus are independently defined as real and local.
In *no* physical naturally occurring continuous phenomenon is this the case. The orbital path of a planet in reverse obeys the same physical laws as in forward, so it does "make sense to imagine that alternative situation." Zeilinger tacitly assumes that an observer wandering into a quantum system has a definition of itself that affects the definition of other particles in the system -- thereby the classical observer creates the quantum reality.
Were that true, the classical and the quantum space would have a definite boundary. Exploring the boundary would require the classical observer to be a quantum object, so the act of measurement would actually change the definition of the observer. This doesn't happen, of course, so one has to assume nonlocality along with entanglement. Because nonlocality violates relativity, one has to assume linear superposition to make nonlocality work.
Things in relation, however, don't depend on entanglement, nonlocality or superposition *at any scale.* Things in relation are scale invariant and coordinate free.
It should have been the simplest thing -- and would have been, were topology as advanced in 1964 as it is today -- to understand that Bell's choice of measure space (the real line) where neighboring relations are linear, is the wrong fit for nature, whose measurement functions are demonstrably complete, continuous and nonlinear.
Joy's simply connected measurement framework fits the observation of strong quantum correlations without assuming a rigged space that applies only to quantum measurement. It's the space in which we live, the space in which we experiment, a space which we are not compelled to imagine exists only in a mystical quantum entangled world.
The question is: Can the simulation of a continuous function be a continuous function? It is, and so the universe is the answer. The metaphysical realism of what exists in relation cannot be other than manifestly local.
Tom
* *The God Particle*
It's been over a month now since the start of this thread, and still the only defender of standard quantum (i.e., probabilistic) theory to come forward is Florin Moldoveanu. His arguments are refuted -- are they the best that can be made?
Referring again to the Pironio, et al, paper linked earlier:
" ... there is no such thing as true randomness in the classical world: any classical system admits in principle a deterministic description and thus appears random to us as a consequence of a lack of knowledge about its fundamental description.
"Quantum theory is, on the other hand, fundamentally random; yet, in any real experiment the intrinsic randomness of quantum systems is necessarily mixed-up with an apparent randomness that results from noise or lack of control of the experiment. It is therefore unclear how to certify or quantify unequivocally the observed random behaviour even of a quantum process."
The authors assume that nonlinear positive feedback (noise) in a quantum system can be mitigated by linear negative feedback on the assumption that quantum theory is "fundamentally random." Because of this assumption, the experimental controls on Bell-Aspect type results are statistically reconciled with the theoretical result (Bell-CHSH inequalities) by the imposition of negative feedback from the *experimenter.* In other words, by disallowing nonlinear positive feedback in the experimental protocol, the experiments validating Bell's theorem beg their own conclusion.
Joy's result shows unambiguously that natural nonlinear random input results in the smooth function of quantum correlations, with no boundary between quantum and classical domains.
Refute that.
Tom
By the way, John Reed has translated Michel Fodje's simulation of my model from Python to Mathematica (just as he translated Chantal Roth's simulation of my model from Java to Mathematica). The code is now much shorter. It can be found here.
Also, I have updated my paper to include a brief discussion of Michel's simulation.
Hi Joy,
For those that have Mathematica, the notebook file by John Reed is here.. Amazing how much more compact it is.
Best,
Fred
Somewhere a programmer is feverishly trying to invent a computer language that does nothing but simulate Bell inequality violations. :-)
Thanks, Fred.
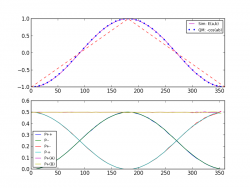
The Mathematica code is indeed quite compact. It also shows how powerful Michel's simulation is. In less than million runs it generates an almost perfect cosine curve. It beautifully complements Chantal's simulation, and puts the final nail in the coffin of Bell's theorem.
Best,
Joy
