This is amazing to me.
Except for some technical programming questions in sci.physics.foundations (which have been addressed and disposed of) I see only internet silence on this simulation that critics IIRC universally said is a prerequisite to having Joy's measurement framework taken seriously.
As they say in American baseball -- what are you waiting for, egg in your beer?
Tom
Tom,
As you may recall, many completely bogus claims were made about my local-realistic framework by those committed to Bell's theorem. This wrongfully undermined my perfectly sound work, misled the physics community, and damaged my scientific reputation. Do you see anyone coming out now and saying that they were wrong? What does that tell you about the true intentions of those who made the wrongful claims? What does that tell you about their scientific and moral integrity? What does that tell you about their ability to judge a perfectly sound work that goes against their cherished beliefs?
Best,
Joy
Joy, I agree. One has to have a personal agenda aside from the good of science to behave this way. Some made their agenda obvious from the beginning. I can't find any excuse for the others.
Leon Lederman and Dick Teresi asked, "If the universe is the answer, what is the question?"*
Non-Realists such as Anton Zeilinger imply that there are no questions at a foundational level. "Zeilinger says that some of the alternative non realist possibilities are truly weird. For example, it may make no sense to imagine what would happen if we had made a different measurement from the one we chose to make. 'We do this all the time in daily life,' says Zeilinger -- for example, imagining what would have happened if you had tried to cross the road when a truck was coming. If the world around us behaved in the same way as a quantum system, then it would be meaningless even to imagine that alternative situation, because there would be no way of defining what you mean by the road, the truck, or even you."
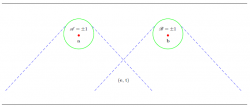
Zeilinger assumes -- as do all Bell's theorem adherents -- that the definition of objects precedes the measurement of correlations between objects. It should be no surprise, therefore, that the assumption of quantum entanglement generates a measurement result based merely on the definition of itself. The proof of the theorem is a nonconstructive tautology.
What Bell loyalists neglect is that there *is* no way of objectively " ... defining what you mean by the road, the truck, or even you." And there doesn't need to be. The realism of continuous functions does not depend on discrete definitions -- in every experiment purporting to show quantum entanglement and violation of Bell/CHSH inequalities, the experimenter and the apparatus are independently defined as real and local.
In *no* physical naturally occurring continuous phenomenon is this the case. The orbital path of a planet in reverse obeys the same physical laws as in forward, so it does "make sense to imagine that alternative situation." Zeilinger tacitly assumes that an observer wandering into a quantum system has a definition of itself that affects the definition of other particles in the system -- thereby the classical observer creates the quantum reality.
Were that true, the classical and the quantum space would have a definite boundary. Exploring the boundary would require the classical observer to be a quantum object, so the act of measurement would actually change the definition of the observer. This doesn't happen, of course, so one has to assume nonlocality along with entanglement. Because nonlocality violates relativity, one has to assume linear superposition to make nonlocality work.
Things in relation, however, don't depend on entanglement, nonlocality or superposition *at any scale.* Things in relation are scale invariant and coordinate free.
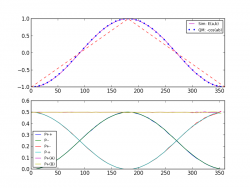
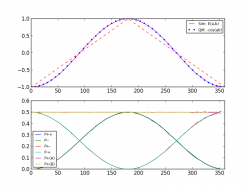
It should have been the simplest thing -- and would have been, were topology as advanced in 1964 as it is today -- to understand that Bell's choice of measure space (the real line) where neighboring relations are linear, is the wrong fit for nature, whose measurement functions are demonstrably complete, continuous and nonlinear.
Joy's simply connected measurement framework fits the observation of strong quantum correlations without assuming a rigged space that applies only to quantum measurement. It's the space in which we live, the space in which we experiment, a space which we are not compelled to imagine exists only in a mystical quantum entangled world.
The question is: Can the simulation of a continuous function be a continuous function? It is, and so the universe is the answer. The metaphysical realism of what exists in relation cannot be other than manifestly local.
Tom
* *The God Particle*
It's been over a month now since the start of this thread, and still the only defender of standard quantum (i.e., probabilistic) theory to come forward is Florin Moldoveanu. His arguments are refuted -- are they the best that can be made?
Referring again to the Pironio, et al, paper linked earlier:
" ... there is no such thing as true randomness in the classical world: any classical system admits in principle a deterministic description and thus appears random to us as a consequence of a lack of knowledge about its fundamental description.
"Quantum theory is, on the other hand, fundamentally random; yet, in any real experiment the intrinsic randomness of quantum systems is necessarily mixed-up with an apparent randomness that results from noise or lack of control of the experiment. It is therefore unclear how to certify or quantify unequivocally the observed random behaviour even of a quantum process."
The authors assume that nonlinear positive feedback (noise) in a quantum system can be mitigated by linear negative feedback on the assumption that quantum theory is "fundamentally random." Because of this assumption, the experimental controls on Bell-Aspect type results are statistically reconciled with the theoretical result (Bell-CHSH inequalities) by the imposition of negative feedback from the *experimenter.* In other words, by disallowing nonlinear positive feedback in the experimental protocol, the experiments validating Bell's theorem beg their own conclusion.
Joy's result shows unambiguously that natural nonlinear random input results in the smooth function of quantum correlations, with no boundary between quantum and classical domains.
Refute that.
Tom
By the way, John Reed has translated Michel Fodje's simulation of my model from Python to Mathematica (just as he translated Chantal Roth's simulation of my model from Java to Mathematica). The code is now much shorter. It can be found here.
Also, I have updated my paper to include a brief discussion of Michel's simulation.
Hi Joy,
For those that have Mathematica, the notebook file by John Reed is here.. Amazing how much more compact it is.
Best,
Fred
Somewhere a programmer is feverishly trying to invent a computer language that does nothing but simulate Bell inequality violations. :-)
Thanks, Fred.
The Mathematica code is indeed quite compact. It also shows how powerful Michel's simulation is. In less than million runs it generates an almost perfect cosine curve. It beautifully complements Chantal's simulation, and puts the final nail in the coffin of Bell's theorem.
Best,
Joy
Much has happened since 2012. At least four explicit, event-by-event, computer simulations of my local model for the EPR-Bohm correlation have been independently produced by different authors, with codes written in Java, Python, Excel Visual Basic, and Mathematica. I discuss two of these simulations in the appendix of the attached paper. A compact translation of one of these simulations (from Python to Mathematica) can be found here.
Each simulation has given different statistical and geometrical insights into how my local-realistic framework works, and indeed how Nature herself works. The original simulation written by Chantal Roth, which is most faithful to 3-sphere topology, may appeal to more geometrically inclined, whereas Michel Fodje's simulation, which has its own unique features, may appeal to more statistically inclined. In the end, however, all of these simulations, together with the original analytical model, confirm what I have been arguing for, for the past six years. The full details of my argument, which concerns the topological origins of quantum correlations, can be found on my blog.
Joy et al,
"The original simulation written by Chantal Roth, which is most faithful to 3-sphere topology, may appeal to more geometrically inclined, whereas Michel Fodje's simulation, which has its own unique features, may appeal to more statistically inclined."
This is what I find the most convincing evidence, that a simulation of a continuous function is a continuous function. Regardless of whether one assumes continuous geometry, or discrete points, correlated and anti-correlated values are locally neighboring elements. That is, no matter how apparently entangled two discrete points of a measurement function may appear -- at any distance scale -- random input correlates the entire wave function to an equilibrium state at every distance scale.
In other words, both evolving discrete particle states (Fermi-Dirac) and static geometry (Bose-Einstein) are reconciled to the same unitary and dynamic spacetime.
The implications go far beyond local microscale quantum correlations of the kind described by Bell's theorem. The quantum and classical measure domains are not independent at any time-distance scale.
Ever since the '30s, researchers have tried to find a transition schema to describe where the discrete measures of quantum theory become a classically smooth function. If such an intermediate function is simply the classically random input that we call quantum decoherence (Zeh, Zurek), then all the fundamentally classical wave interactions (reinforcement, destruction, interference) are represented as nonlinear input to the linear order of particle states.
All best,
Tom
Hello All,
I have attached some notes on Bott Periodicity and Cli fford Algebras from Kyler Siegel, which are of general interest or relevance to this forum topic, but also partially answer the question raised by James Putnam above. He asks if I am talking about "'spaces', in addition to but external to our observed universe" and I must answer that instead it only appears that our universe has 3 Euclidean spatial dimensions plus time, because of the way objects are embedded in spacetime, which relativists see as a curved fabric. And what Joy proposes is that this 4-d fabric is topological, with a geometry that is non-commutative.
Instead of being external to the universe; perhaps the higher-dimensional reality is what underlies or gives rise to the appearance of 3-dimensional objects and space. The thing about parallelization is that it gives the fabric a particular weave - a specific warp and weft for any orientation of a suitably situated observer and/or apparatus. This also produces what appear to be non-local quantum correlations. Of course; if the universe has a parallelized topological fabric, this also accomplishes flatness, and so gives the universe the appearance of a Euclidean local geometry. The paper explains why only specific geometries accomplish this.
I think that is what Joy is talking about.
JonathanAttachment #1: BottPeriodicityAndCliffordAlgebras.pdf
I think this will help too..
I attach the slides for Michael Atiyah's lecture at the Simons Center, that covers some of the same material as his talk at the IAS which is referenced by Joy in the introduction for this thread. This speaks to the question of why higher dimensions and higher-order algebras are a part of the natural order. It will also help to explain why some of what Siegel says in his notes above is important stuff to Physics people - or should be.
Regards,
JonathanAttachment #1: 20101103_Atiyah_-_From_Algebraic_Geometry_to_Physics.pdf
Hi Johnathan,
I don't agree with slide 17 in the first attachment above. I believe octonions are necessary for the triality (3-handedness) in the QCD (strong) sector. Gravity is emergent from the Standard Model if interpreted correctly.
Best,
Fred
Let me add a light-cone picture to make this clear:
Oh, well. The picture is too small to see that the initial state (e, t) defined by the set above is in the backward light-cone of both Alice and Bob, and every particle in the state (e, t) ends up being detected by either Alice or Bob, with 100% detector efficiency.
Jonathan,
Thanks for the lovely slides. Makes me wish I had been at the lecture.
I want to pick one nit with your post -- quantum correlations never appear nonlocal. Nonlocality is an assumption of quantum mechanics, to describe results of "the experiment not done" that supposedly imparts action at a distance.
Delighted to see that Sir Michael Atiyah addresses the necessity to incorporate both retarded and advanced solutions to the wave equation.
Best,
Tom
Excellent remarks..
I think the retarded and advanced solutions correspond with the warp and weft in the comment above, Tom, or align with the fabric to give it a specific weave. I agree with Fred's remarks regarding octonions and QCD and I would add that strong force binding and gravitational attraction may be the short-range and long-range manifestation of the same force, which would necessitate such a linkage.
And in reaction to your other comment, Tom; I think the assumption of non-locality by QM folks, as an explanation for correlations at a distance, is perfectly sensible - if one ignores the possibility that the fabric itself could be non-commuting - but appears naive when it is seen that a non-commutative spacetime geometry is actually natural or reasonable.
Again; it's that darn point at infinity which is not correctly reckoned for. In effect; it is the far edge of the universe that sets the local scale of objects. But to think about things this way turns our perceptions inside out, or makes us see the fabric of spacetime that way, when one needs to see that fabric from the outside in - to know its nature.
Regards,
Jonathan
Hello Joy,
Good to hear of the computer simulations confirming your results! Shouldn't it also be possible to confirm this experimentally? From what I understand of your results you mathematically show quantum correlations to be dependent on the geometry of the experimental apparatus. While Bell assumes a "flat" geometry you use "spheres". Any way such design be tested confirming your predictions?
Best wishes,
Constantinos
Hi Constantinos,
Glad to see you are still following this debate. It is indeed good to have several computer simulations confirming my model and its predictions. If nothing else, they prove the critics of my work wrong, as Tom points out.
In the end, however, a computer simulation is only a model of the real thing---a numerical model. Even my original analytical model is just that---a mathematical model. So you are quite right to raise the issue of a real experiment. I have indeed proposed an experiment to provide a final decisive test of my argument against Bell's. Please see section IV of the attached paper for details. Conceptually the proposed experiment is very simple. And it would cost no more than 200,000 dollars---which is peanuts compared to the amount of money required for experiments these days.
Best wishes,
