Sorry for the repetition.
I didn't realize until I hit submit that I'd used 'but' so many times in a row.
It sounds silly, but you all know what I mean. (there I go again)
Regards (no ifs, ands, or buts),
Jonathan
Sorry for the repetition.
I didn't realize until I hit submit that I'd used 'but' so many times in a row.
It sounds silly, but you all know what I mean. (there I go again)
Regards (no ifs, ands, or buts),
Jonathan
Thank you, Jonathan.
Those are two quite useful references.
Some things are worth repeating. Such as this from Grisha Perelman:
"It is not people who break ethical standards who are regarded as aliens. It is people like me who are isolated."
I hope the power elite has conscience enough to learn something from Perelman.
Best,
Joy
It is evident..
In the case of Grisha Perelman and in that of Joy Christian and Bell's theorem interpretation disproofs, what is featured are unifying properties of nature, or unifying features present in the structure of Math itself. One can't really get around the existence of these things, in terms of their ubiquity or universality.
Until recently; I'd have heard the words 'Frobenius conjecture' and said "No thanks, I'll stop there; that's a bit too deep or abstruse for me." Likewise with Poincare, for many people. But once you grasp the proof of certain conjectures; you realize why certain things are intuitively obvious or self-evident, as something that must be true, to a great mind.
All the Best,
Jonathan
I guess I should say..
Regarding the Frobenius papers. Given that one was published in 1991 and the other in 2000, the conclusive evidences have been on the table for long enough that the implications of such proofs are noteworthy as truths. Also with Perelman's proof; it leads inexorably to certain truths about reality and the internal structure of Math, which MUST apply on some level to Physics.
I can clearly state that a lot of what you have set out, Joy, is a direct outgrowth of that applicability. Is your usage exactly correct, in terms of recreating the Physics phenomenology precisely. Who knows? But some of the correct ideas and motives are there. What I am learning now will help me to discuss these things in a more informed manner, however.
All the Best,
Jonathan
An addendum (tongue in cheek)..
Maybe you are tolerated by FQXi, Joy, because Max Tegmark sees your theory as the ultimate fulfillment of the Mathematical Universe Hypothesis, and secretly hopes that you turn out to be precisely correct.
Regards,
Jonathan
In the beginning there was no math. Then came sedonions, then octonions, then quaternions, then complex numbers and finally the real numbers. Humans discovered what nature created in reverse order.
Best,
Fred
Jonathan,
Thanks for bringing up the Frobenius conjecture (theorem) and especially the Feldman paper.
It has troubled me since the beginning of this affair, that the mathematics Joy employs is little understood in terms of how dimensionality affects relations among points of geometric objects (generalized to topology) where the function is continuous and not degenerate. It's been a great source of frustration to me personally that there was (and apparently continues to be) a lack of understanding that a measurement function continuous from an initial condition is independent of linear parametrization. In other words, the singular initial condition (such as Bell's theorem dependence on observer orientation) does not constitute an element of the function, because it is discontinuous from the nondegenerate measure space.
My own research attempts to show by an arithmetic method how random nonlinear input smooths the function, proving the lemma: An indefinite relation between two distinct odd primes implies one parametrically definite relation.
All best,
Tom
Got to have a closer look at that!
Someone didn't like my previous post. No matter.
Below is a sneaky peak of the *fourth*, explicit, event-by-event, simulation of my local model for the EPR-Bohm correlation---this time the code written (independently) in Python (the previous simulations were written in Java, Excel Visual Basic, and Mathematica). The details of the simulation will follow soon.
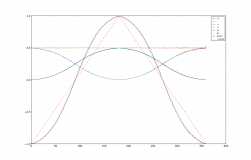
The model can be found in the attached paper.Attachment #1: 20_whither.pdf
Joy, can you give a closer look? Looking forward to the details.
Tom,
The work on the latest simulation is still in progress. I will post the details soon.
On a different note: What happened to my previous post reminded me once again of the quote from Grisha Perelman you posted earlier: "It is not people who break ethical standards who are regarded as aliens. It is people like me who are isolated."
Best,
Joy
Hi Joy,
I have not shown much interest in your work as I have am inclined to believe like Einstein that QM is incomplete. As a result discussions for and against Bell's theorem have not ignited any interest in me. Moreover most of the discussions are conducted in mathematical language, which like all languages can equally be used to tell lies or tell the truth. I recently took a peek at your site and it appears like Einstein you are on the side of locality and realism so I think I can engage.
To start this engagement, in Fig.1.1 "The Point Bell Missed", you said this statement is fundamental and I am in full agreement. The statement is "Although lines and planes contain the same number of points..."
What does this mean?
Firstly, do lines contain points? And if so, are these numbered? If numbered, how are they to be counted, to know and assert that lines and planes have the SAME number?
Note that I am not a critic of your work neither am I currently endorsing it. It all depends...
Akinbo
*By the way your Bio is impressive so I believe you can unearth the truth.
Hi Joy,
As the news gets better and better for the predictions of EPR, the critics seemed to have retreated into a cone of silence.
Nothing could be more compelling than successful simulations run now in at least five machine languages. I am surprised and impressed.
All best,
Tom
Akinbo,
You are misunderstanding. Joy's work supports EPR and opposes the idea that quantum mechanics is a complete theory. In fact, it is quite easy to show that QM is incomplete. The real foundational question is whether reality is inherently probabilistic ("God plays dice") or determined by hidden variables imposed by nature independent of the observer.
So far as the correspondence of points and lines, these are basic theorems in geometry. There are as many points in this line: ___, as there are in the entire universe.
Best,
Tom
Tom,
As I posted I am in support if 'Joy's work supports EPR and opposes the idea that quantum mechanics is a complete theory'. The support is however qualified so that we don't substitute one incomplete work with another. For example, I have suggestions on what can be HIDDEN, LOCAL, VARIABLE and REAL that Joy can investigate. That way, a local hidden variable theory can explain the incompleteness of QM. Now we may not be able to identify this agency if as you say, we rely on the premise that "There are as many points in this line: ___, as there are in the entire universe".
How many of these your lines ___ ___ ___ ___ ___ are in this message box and how many of this message boxes are in your line?
If your line and the message box contain the same number of points, then you should be able to fit the message box into your line topologically, talk less of letting your line contain the universe.
Regards,
Akinbo
Akinbo,
"The support is however qualified so that we don't substitute one incomplete work with another."
Rest easy, then, because relativity -- the special and general theory -- is mathematically complete.
I am not going to discuss the point-line thing in this forum. It's well understood geometry.
Best,
Tom
Rather than being quite so dismissive..
I might recommend a look at what Atiyah and Sutcliffe have to say about Point Particles, in the attached paper. Besides; the point to consider here is the one at infinity that, as you love to remind us Tom, is a defining element of projective spaces. The magical thing about parallelized S3 and S7 is that they connect proximal and distal space seamlessly. So the difference between collinear and non-collinear points is an essential and sometimes subtle distinction - that is certainly germane to this discussion. Does topological space have thickness? Approaches to quantum gravity with this feature have been suggested (e.g. - Arkani-Hamed, Dvali, Dimopolous).
But as for the question of infinite divisibility, people tend to believe Dedekind without fully understanding what his method was about, or trying to understand, and just consider the matter settled. Certainly though; the experts have been around the block with this issue, and the consensus is that ANY finite span on the number line DOES contain an infinite range - in that it is endlessly sub-dividable. The real question (pun intended) is whether nature offers us an unbroken span. I think Joy's topological approach may absolve us of the need to quantize space, in order to reconcile things, so that is the question here.
Regards,
JonathanAttachment #1: 0105179.pdf
Thanks, Jonathan.
The results of the latest simulation of my model are getting better and better.
Here is the latest version (the details still to come):
Best,
Joy
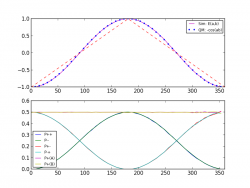
Thanks Jonathan for the journal reference, although my mathematical credentials are not excellent.
You say, "I think Joy's topological approach may absolve us of the need to quantize space, in order to reconcile things,...".
I beg to disagree, while a topological approach may help, Joy's approach MUST NOT shy away from its clear responsibility having started his work with a statement like... "The Point Bell Missed" and "Although lines and planes contain the same number of points...".
Firstly, this statement admits that lines and planes consist of points.
Secondly, by saying the points are numbered is to say they are discrete. Only discrete things can be numbered.
Thirdly, a line is claimed to be 1-dimensional and a plane 2-dimensional. How is a 0-dimensional object contained in a 1-dimensional one? Are the points in a line and those in a plane of same dimension?
Fourthly, the claim that lines and planes contain the SAME number of points needs to be clarified. Is it supportive of what Tom said that "...There are as many points in this line: ___, as there are in the entire universe" and "I am not going to discuss the point-line thing in this forum. It's well understood geometry". What Tom is saying is that number of points on the line is infinite and the number in the universe is infinite, so both the line and the universe contain the SAME number.
The question I would have asked Tom, but can't since he says for him the case is closed is, whether his line, ___ and a segment of it also contain the SAME number of points. If so, whether points can then be said to be capable of being counted as to make assertions like two geometrical objects having the same number as Joy started with.
Jonathan, henceforth we must demand strict definition of what anyone, particularly the more mathematically inclined are asserting. It is from not being as demanding that mathematicians were allowed to introduce 'a line having length but with a breadth of absolute zero' and a 'surface of absolute zero thickness' into our physics.
Akinbo
Jonathan,
I always appreciate your ability to get to the nub of the issue. "I think Joy's topological approach may absolve us of the need to quantize space, in order to reconcile things, so that is the question here."
Indeed, I think so as well. I was disheartened that Vesselin Petkov's entry a couple of essay contests ago ("Can spacetime be quantized?"), didn't get near the attention it deserved.
At the end of the day -- at a foundational level -- we can discard the idea of particles, though we cannot discard the continuum.
The Dedekind cut principle is one my favorite mathematics results, and I agree with you that it is ill understood, even often misinterpreted. Dedekind says that, e.g., there exist two numbers whose product is sqrt2, even though one cannot provide a procedure for multiplying the two. By existence, however, because sqrt2 is an algebraic number, we are assured the computability of corresponding points by which 2(sqrt2) sets an upper bound of correlation . The current proliferation of computer simulations of Joy's framework is rich confirmation. That's only the beginning -- aside from mere computability, Joy's research promises to tell us what "quantum" really means.
All best,
Tom